Seitenhalbierende
Seitenhalbierende konstruieren vom Mittelpunkt der Seiten durch den gegenüberliegenden Eckpunkt. Der Schnittpunkt davon ergibt den Schwerpunkt des Dreiecks.
Themensammlung rund um Inhalte der Mathematik. Chronologische Anordnung der neusten Beiträge
Seitenhalbierende konstruieren vom Mittelpunkt der Seiten durch den gegenüberliegenden Eckpunkt. Der Schnittpunkt davon ergibt den Schwerpunkt des Dreiecks.
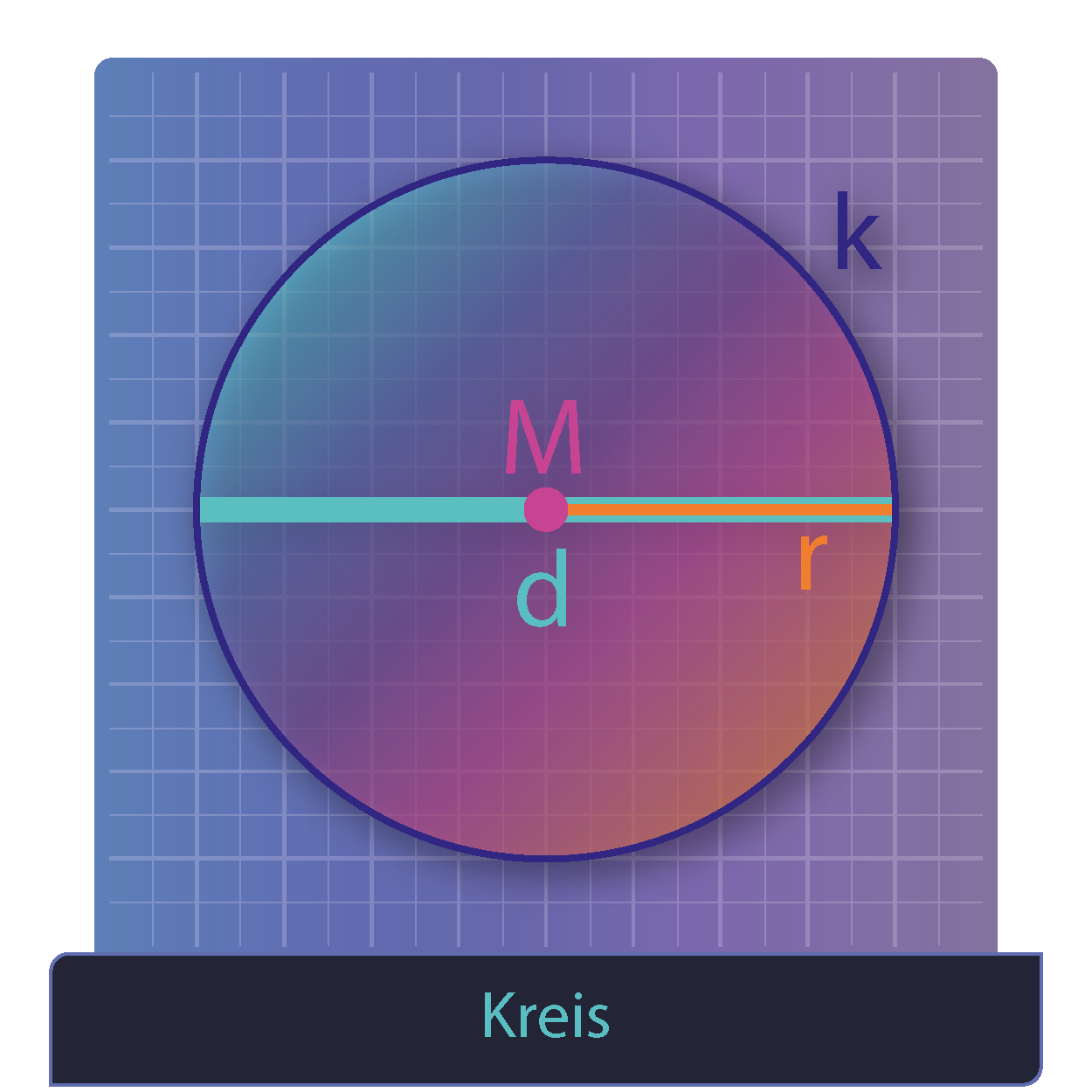
Hier eine Sammlung von Beispielaufgaben mit Lösungen. Die Aufgaben zum Konstruieren greifen ddas Gelernter auf und können interaktiv abgespielt werden.
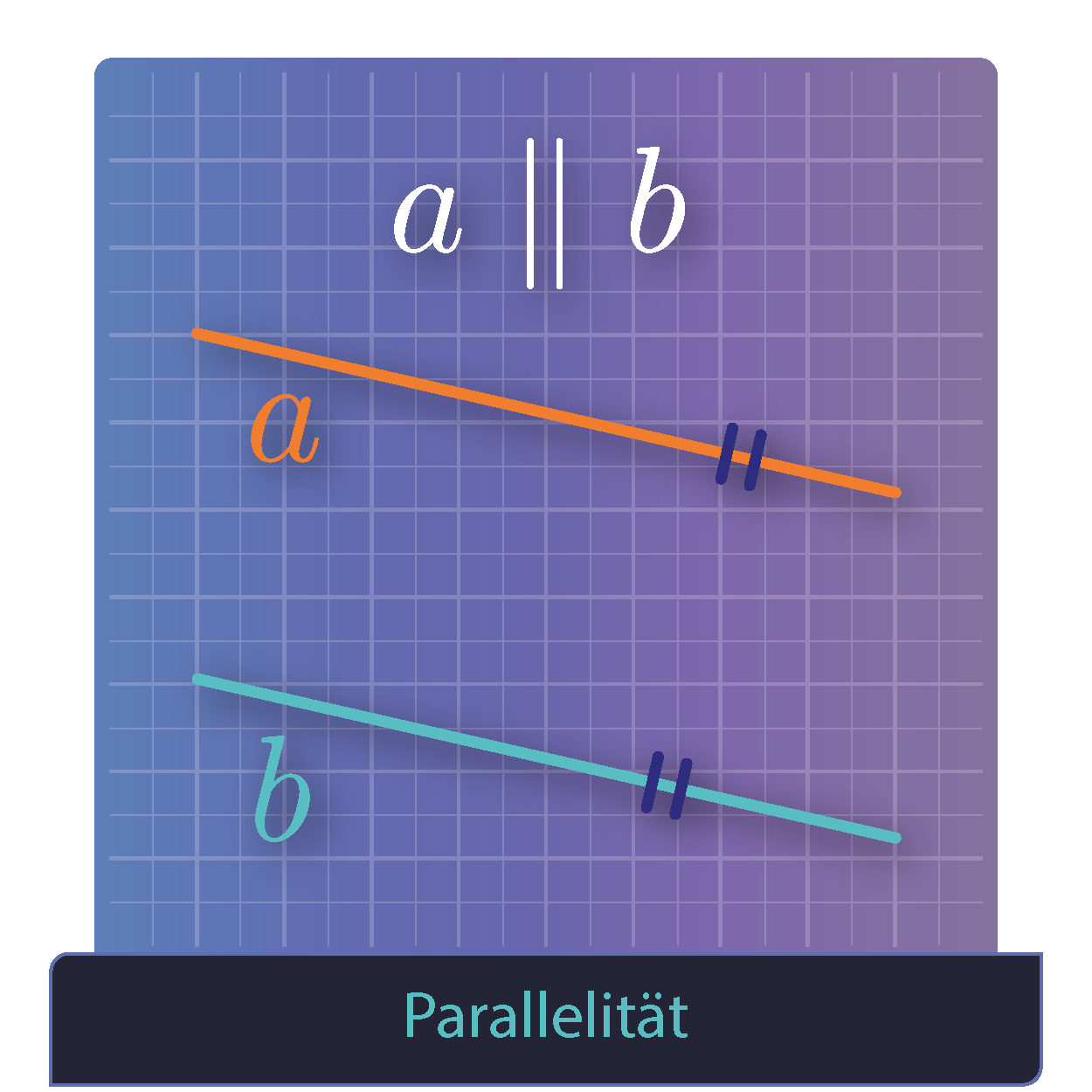
Parallele konstruieren mit Zirkel und Lineal. Anschauliches und interaktives Beispiel zum selber nachvollziehen/ausprobieren der Konstruktion durch einen Punkt.
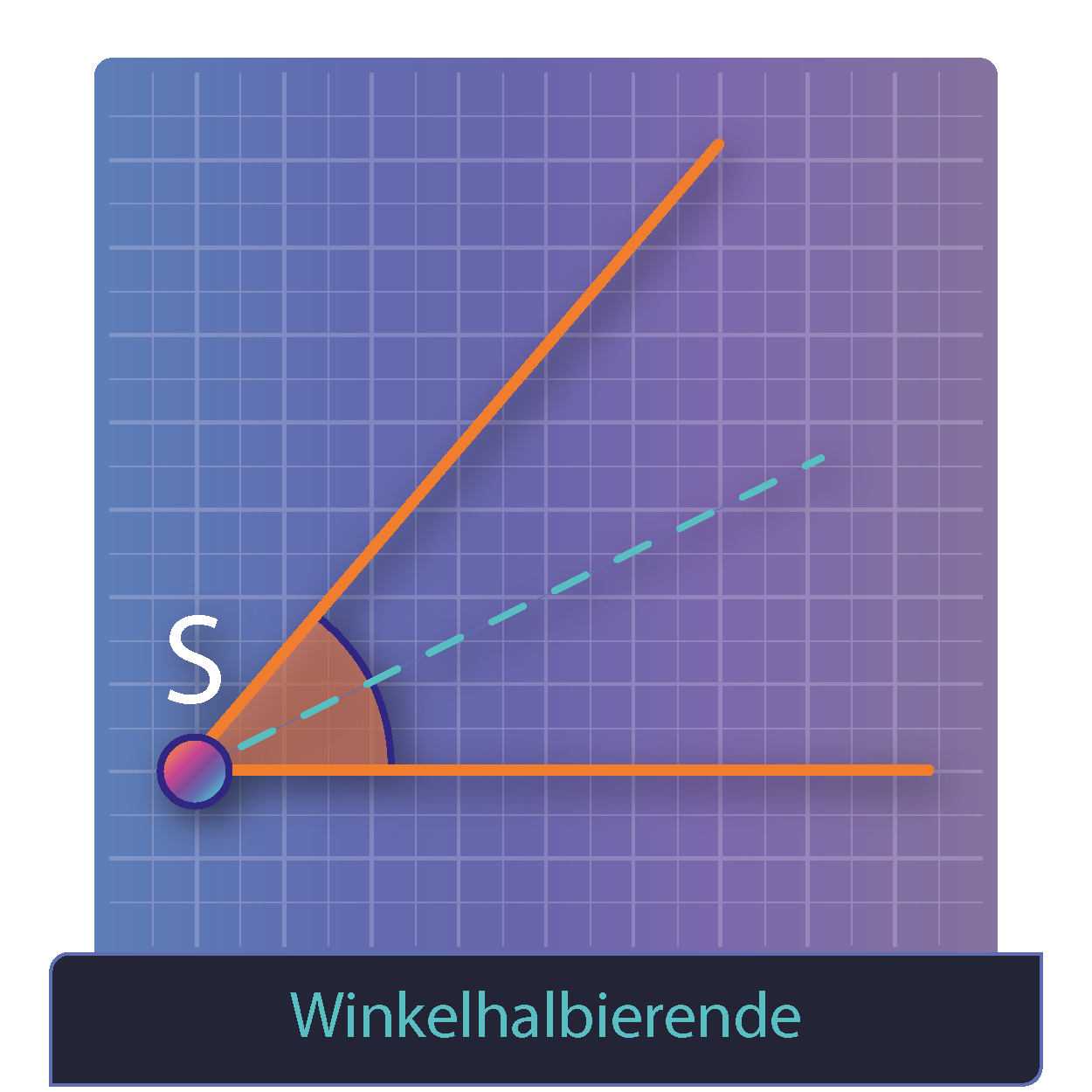
Definition und Konstruktion der Winkelhalbierenden nur Zirkel und Lineal ohne Geodreieck! Die Winkelhalbierende verläuft zwischen den beiden Schenkeln des Winkels durch den Scheitelpunkt.
Winkel konstruieren ohne diesen zu messen. Der Zirkel als Hilfsmittel reicht aus, um einen beliebigen Winkel exakt zu übertragen! Hier selber ausprobieren.
Konstruktion der Senkrechten nur mit Zirkel und Lineal! Interaktives Beispiel einer Mittelsenkrechten bzw. Orthogonalen auf einer Strecke und durch einen Punkt.
Ein Viereck ist erst einmal eine unpräzise Beschreibung. Verschiedene Eigenschaften der Seiten, Längen oder Winkel bestimmen ein Viereck erst genauer.
Summenregel der Teilbarkeitsrelation. Beispielhaft erklärt durch eine figurierte Darstellung. Erklärung und Anwendung der Summenregel mit einem Beweisvideo.