Winkel mit Hilfe der Winkelsumme berechnen
Hier sind verschiedene zufällige und interaktive Beispielaufgaben vorgestellt zum Thema Winkelsumme berechnen.
Die Aufgabensammlung wird laufend ergänzt.
Die Lösungen und der Lösungsweg zur Berechnung sind immer mit ausgeführt, mit den entsprechenden Links zum Nachlesen und Vertiefen!
Die Aufgaben sind alle zufällig generiert und können durch ein erneutes Laden der Webseite jederzeit zurückgesetzt werden.
Als Eingabe reicht die Zahl ohne Grad-Zeichen!
Aufgaben Winkelpaare
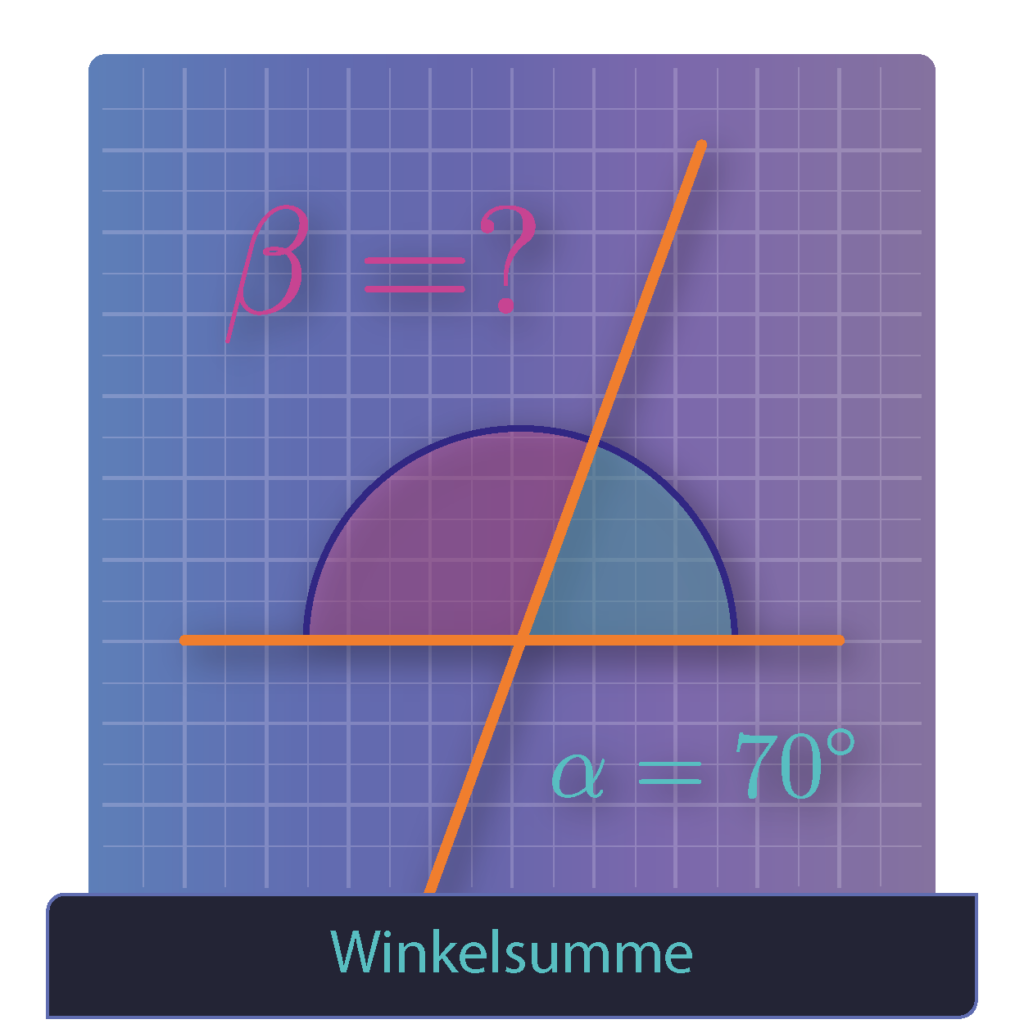
Zur Berechnung wird der Nebenwinkelsatz benötigt.
Nebenwinkel ergänzen sich immer zu 180°!
Also können den Winkel \(\beta\) ausrechnen mit Hilfe des Winkels \(\alpha\).
\(\beta=180°-\alpha\)
Zur Berechnung wird der Scheitelwinkelsatz benötigt.
Scheitelwinkel liegen an sich zwei kreuzenden Geraden gegenüber und sind immer gleich groß!
Also können den Winkel \(\alpha’\) ganz einfach bestimmen, da dieser genau gleich groß ist.
\(\alpha=\alpha’\)
Die Berechnung des Winkels kann entweder über den Nebenwinkelsatz oder über den Scheitelwinkelsatz erfolgen.
Als Nebenwinkel ergänzt dieser den Winkel \(\beta\) wieder zu 180°
Als Scheitelwinkel muss erst der Nebenwinkel zu \(\beta\) berechnet werden (dieser liegt wie \(\beta\) über der Geraden. Und dann kann der Winkel \(\alpha’\) daraus bestimmt werden.
Auch hier gibt es wieder mehrere Lösungswege. Der Winkel \(\alpha’\) kann durch seinen Nebenwinkel zu 180° ergänzt werden. Dieser Nebenwinkel ist dann der Wechselwinkel zu \(\beta\)
Als Nebenwinkel ergänzt dieser den Winkel \(\alpha\) zu 180°.
Wechselwinkel sind gleich groß. Kennen wir also den Nebenwinkel zu \(\alpha’\), dann kann auch \(\beta\) bestimmt werden.
Als Scheitelwinkel muss erst der Nebenwinkel zu \(\beta\) berechnet werden (dieser liegt wie \(\beta\) über der Geraden. Und dann kann der Winkel \(\alpha’\) daraus bestimmt werden.
Aufgaben Winkelsumme Dreieck
Die eingezeichnete Höhe im Dreieck teilt das Dreieck in zwei weitere Dreiecke. Dadurch reicht es das rechte Dreieck zu betrachten.
Mit Hilfe der Winkelsumme im Dreieck kann dann der Winkel \(\delta\) bestimmt werden.
\(\delta = 180° – 90° – \beta\)
Zuerst muss der Winkel \(\beta\) bestimmt werden. Nebenwinkel ergänzen sich immer zu 180°.
\(\beta = 180° – 90° – \delta\)
Der Winkel \(\gamma\) wird dann wieder mit Hilfe der Winkelsumme des Dreiecks berechnet.
\(\gamma = 180° – \alpha – \beta\)