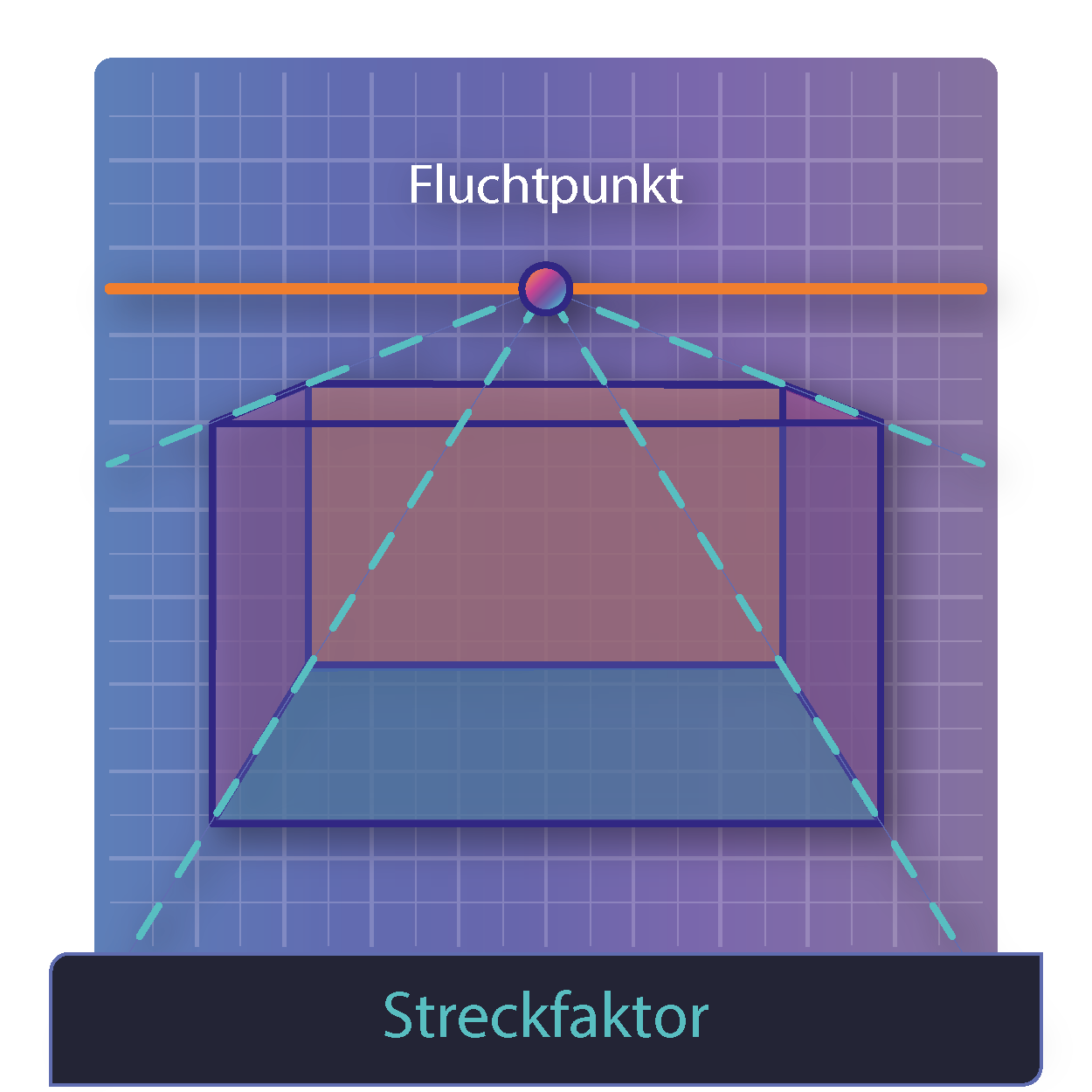
Streckfaktor
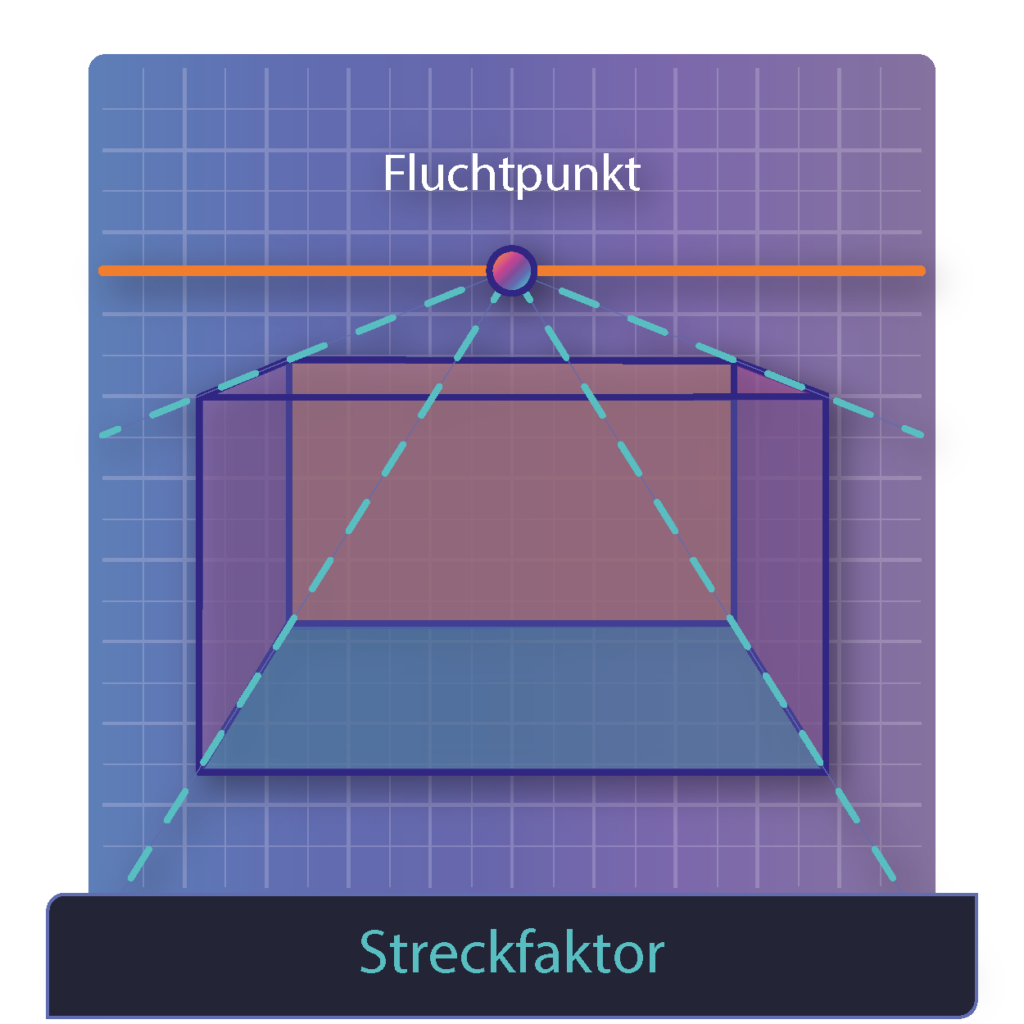
Der Streckfaktor k gibt an, wie eine Figur durch eine zentrische Streckung vergrößert oder verkleinert abgebildet wird.
Allgemein bekannt aus der Kunst, mit einem Fluchtpunkt und Fluchtlinien, um eine Zentralperspektive abbilden zu können.
Zentrische Streckung
Bei der zentrischen Streckung verläuft jeder Bildpunkt durch eine Gerade und durch das Streckzentrum Z.
- Original- und Abbildstrecken sind parallel zueinander
- Winkel sind gleich groß
- Der Abstand bzw. die Länge beträgt den Streckfaktor k
Formel für den Streckfaktor k:
\(k=\frac{ \overline{ZP‘}}{\overline{ZP}}\)
Formel für den Zusammenhang zwischen den Strecken und dem Streckfaktor (umgestellt):
\(k * \overline{ZP} = \overline{ZP‘}\)
Streckfaktor bestimmen
Um den Streckfaktor k zu bestimmen gibt es die folgende Formel:
\(k=\frac{ \overline{ZP‘}}{\overline{ZP}}\) für das Beispiel:
\(k=\frac{\overline{ZB‘}}{\overline{ZB}}=\frac{10,5}{3,5}=3\)
Damit wurde für das Beispiel der Streckfaktor 3 bestimmt.
Um die Strecke x zu berechnen, kann die Formel einfach umgestellt werden zu:
\(k=\frac{\overline{ZP‘}}{\overline{ZP}} \quad \Leftrightarrow \quad k * \overline{ZP} = \overline{ZP‘}\) im Beispiel:
\(k*\overline{ZC} = 3*3,91=11,73cm= \overline{ZC‘}\)
Damit wurde die Strecke von \(\overline{ZC‘}\) berechnet. Jetzt muss nur noch die Strecke von \(\overline{ZC} = 3,91cm\) abgezogen werden für die Strecke x.
\(x = \overline{ZC‘} – \overline{ZC}\)
\(x = 11,73 – 3,91 = 7,82cm\)
Eigenschaften der zentrischen Streckung
Parallelentreue
Die zentrische Streckung ist parallelentreu!
Hier im Beispiel die beiden Geraden \(g ~ und ~ g’\).
Durch die Abbildung der zentrischen Streckung bleibt das Verhältnis gleich und die Parallelität bleibt bestehen.
Winkeltreue
Die zentrische Streckung ist winkeltreu!
Die Größe der Winkel bleibt bei der Abbildung gleich, weil die Größe der eingeschlossenen Schenkel identisch ist.