Winkelhalbierende konstruieren
Nachdem in einem anderen Artikel erläuter wurde, wie ein Winkel konstruiert werden kann, geht es hier darum, eine entsprechende Winkelhalbierende zu konstruieren.
- Die Winkelhalbierende verläuft durch den Scheitelpunkt des Winkels
- Diese verläuft mittig
- Teilt den Winkel in zwei deckungsgleiche Teile
- Die Winkelhalbierende agiert auch als Symmetrieachse
Unten ist die entsprechende Konstruktion nachgebildet. Hier ist die Konstruktion mit Hilfe eines Zirkels nachgebildet.
| Winkelhalbierende | verläuft durch die Mitte des Winkels |
| Ursprung | in der euklidischen Geometrie |
| Bezeichnung | Halbgerade durch den Scheitelpunkt |
| Werkzeuge zum Konstruieren | Zirkel und Lineal ohne Maßeinheiten zum Messen |
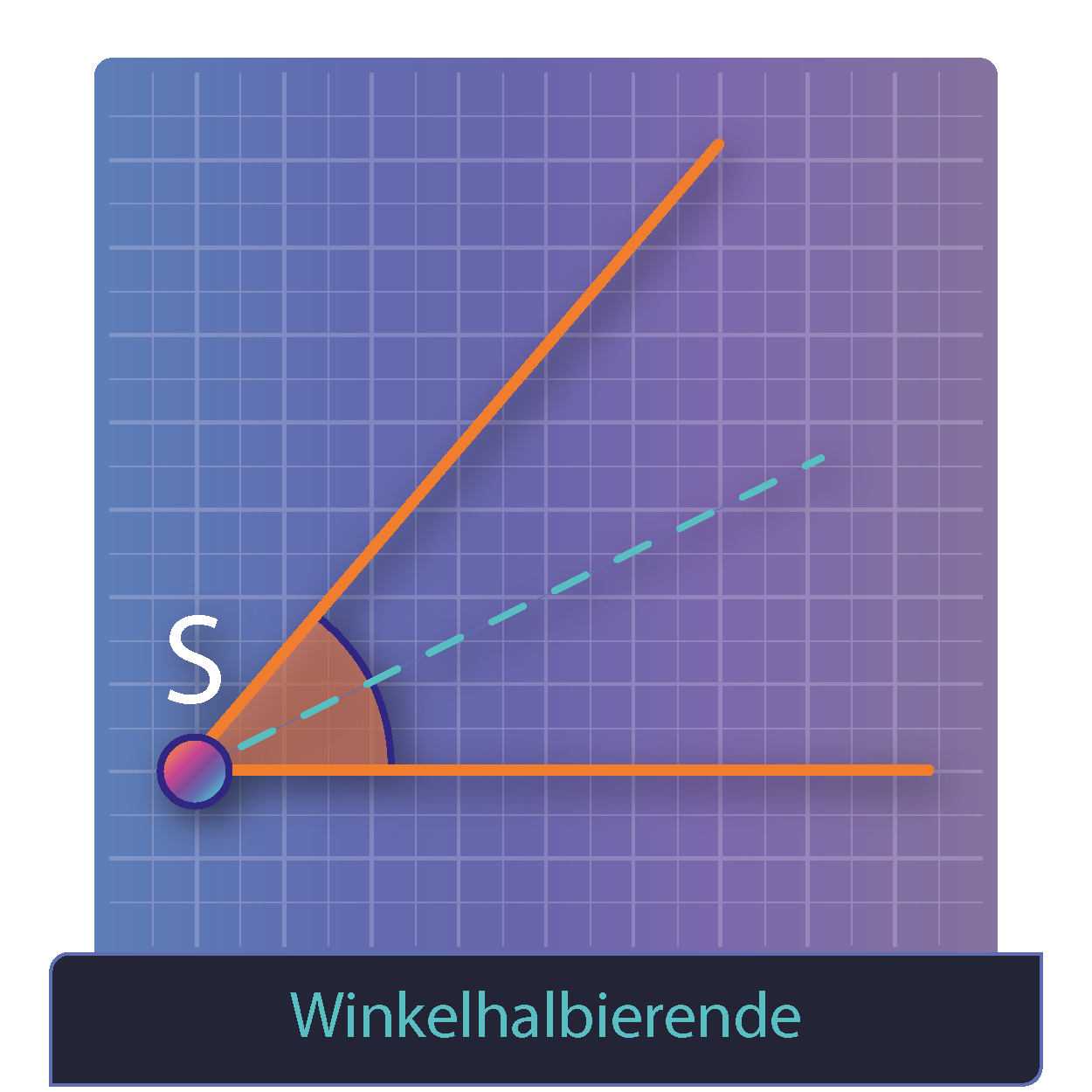
Winkelhalbierende konstruieren
Durch die begrenzten Hilfsmittel für die Konstruktion, wird auch hier die Konstruktion mit Hilfskreisen erstellt!
Um die Winkelhalbierende zu konstruieren, sind folgende Schritte notwendig:
- Einen beliebig großen Kreis um den Scheitelpunkt S konstruieren.
- Es entstehen Schnittpunkte mit den Schenkeln des Winkels.
- A und B markieren
- Jetzt um die Schnittpunkte A und B jeweils einen Kreis zeichnen, mit dem Radius\(\overline{AB}\))
- Die beiden Kreise haben jetzt auch wieder Schnittpunkte.
- Einen Schnittpunkt mit C markieren
- Eine Gerade einzeichnen durch C und S
- Die Winkelhalbierende ist konstruiert!
Unten in dem Feld kann die Konstruktion einmal schrittweise abgespielt werden!
Besondere Merkmale
Hier im Beispiel kann die Winkelhalbierende verändert werden, um die Eigenschaften besser zu verstehen.
Hier im interaktiven Beispiel liegt der Punkt P auf der Winkelhalbierenden. Dieser kann frei verschoben werden, um den gleichbleibenden Abstand zu den Senkrechten als Symmetrie zu veranschaulichen.
Rückblick Konstruktion
Das Konstruieren ohne Geodreieck oder Maßband (zum abmessen) bietet die Möglichkeit, dass eine exakte Darstellung gelingt. Da nichts abgemessen werden kann, müssen einzelne Schritte kombiniert werden.
Das bietet die Möglichkeit, dass der Zusammenhang leichter verstanden werden kann, da eine Konstruktion viele Kompetenzen und Eigenschaften abverlangt!