Grundbegriffe und Definitionen
| Die Elemente | Abhandlung „Elemente“ 3. Jhd. v. Chr. von Euklid |
| Euklid | griechischer Mathematiker, ca 360 v. Chr in Athen geboren |
| Elementargeometrie | Geometrie aus dem griechischen ~ Erdmessung |
Allgemeine Begriffe der Geometrie
Hier wird ein grober Einblick in die Begriffe der verwendeten Bezeichnungen der Elementargeometrie gegeben.
Punkte, Strecken und Winkel werden näher beleuchtet und die allgemeinen Konventionen der Schreibweisen werden genannt.
Die Darstellung erfolgt häufig in einem geeignetem Koordinatensystem.
Punkt
Ein Punkt ist, was keine Teile hat.
Konvention:
- Darstellung: mit einem Kreuz: x um den Punkt zu markieren
- Bezeichnungen: mit einem großen Buchstaben: A, B, C, D …
Eigenschaften:
- Der Punkt hat eine exakte Position (Koordinate)
Linie
Eine Linie ist eine breitellose Länge.
Konvention:
- Bezeichnung: mit einem kleinen Buchstaben: f, g …
Eigenschaften:
- Eine Linie muss nicht gerade sein!
- Eine Linie hat eine unendliche Punktmenge
- Eine Linie muss nicht enden
Strecke
Eine Strecke ist eine gerade Linie, die durch zwei Endpunkte begrenzt ist.
Konvention:
- Schreibweise \(\overline{AB}\) um die Strecke zu bezeichnen
- Schreibweise \(\left |\overline{AB}\right |\) um den Abstand zwischen den Endpunkten der Strecke zu bezeichnen
Gerade
Eine Gerade hat weder einen Anfangspunkt noch einen Endpunkt.
- Eine Gerade ist in beide Richtungen unbegrenzt
- Bezeichnung: mit einem kleinen Buchstaben: f, g …
Strahl
Ein Strahl wird durch einen Punkt auf einer Seite begrenzt.
Konvention:
- Bezeichnung als Strahl oder Halbgerade
- Punkt zur Begrenzung dient als Anfangspunkt
- Ein Punkt auf einer Geraden teilt diesen in zwei Strahlen mit gemeinsamen Anfangspunkt
Lagebeziehungen
Sammlung von Beziehungen zwischen geometrischen Objekten.
Die Konvention der mathematischen Schreibweise ist unten angegeben.
Die folgenden Lagebezeichnungen sind möglich:
Zwischen Punkt und Gerade
Punkt auf Gerade:
\(P \ \epsilon \ g\rightarrow P \ ist \ ein \ Element \ von \ f\)
„Die Gerade f geht durch den Punkt P“
Punkt nicht auf Gerade:
\(Q \ \notin \ g\rightarrow Q \ ist \ kein \ Element \ von \ g
\)
„Die Gerade g geht nicht durch den Punkt Q“
Zwischen Geraden
Parallelität:
Geraden sind parallel, wenn sie keinen gemeinsamen Punkt haben oder identisch sind.
\(f \parallel g\)
„f ist parallel zu g“
Schnittpunkt:
Wenn sich zwei Geraden schneiden, haben sie einen Schnittpunkt S.
Wenn die Geraden sich senkrecht bzw. orthogonal schneiden, schneiden sie sich in einem rechten Winkel (90°)!
\(h \perp i\)
„h ist senkrecht zu i“
In der Zeichnung wird der rechte Winkel mit einem Punkt • gekennzeichnet.
Die Beziehungen sind ambig. Wenn f parallel zu g ist, ist auch g parallel zu f.
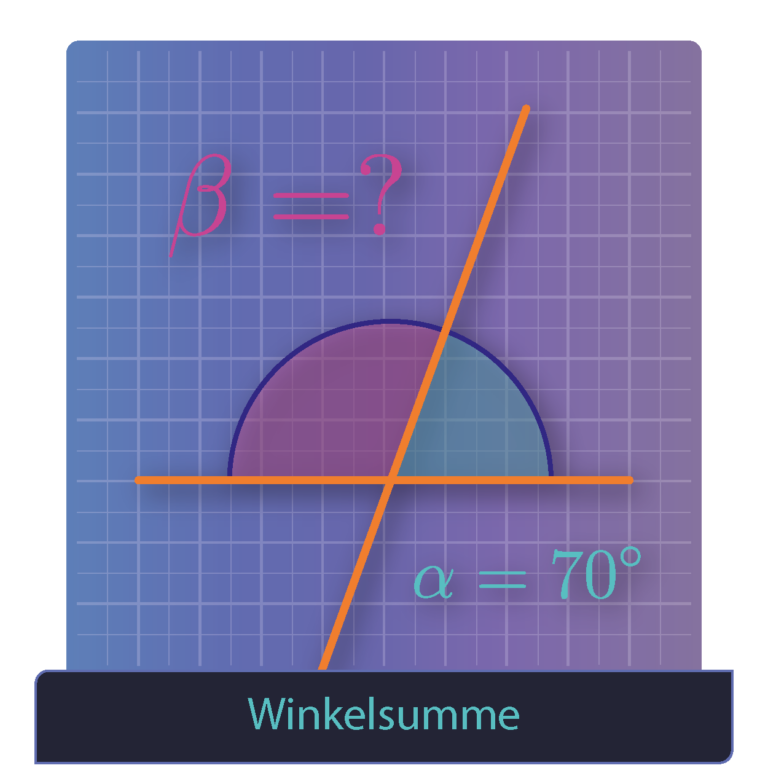
Winkel
| \(\alpha\) | Alpha |
| \(\beta\) | Beta |
| \(\gamma\) | Gamma |
| \(\delta\) | Delta |
| \(\epsilon\) | Epsilon |
| \(\zeta\) | Zeta |
| \(\eta\) | Eta |
| \(\theta\) | Theta |
| \(\iota\) | Iota |
| \(\kappa\) | Kappa |
| \(\lambda\) | Lambda |
| \(\mu\) | My |
| \(\nu\) | Ny |
| \(\xi\) | Xi |
| \(\pi\) | Pi |
Winkelbezeichnungen
Konvention:
- Winkel werden mit griechischen Kleinbuchstaben beschriftet.
- z.B. mit \(\alpha, \beta, \gamma\)
- Können ausgedrückt werden durch die beiden Strahlen die den Winkel ergeben
- ∡ (p,q)
- Winkel können auch durch die Punkte angegeben werden. Beispielsweise mit
- \(\angle ABC\)
- Auch hier immer beachten, dass die Benennung gegen den Uhrzeigersinn verläuft. Sonst wird womöglich ein anderer Winkel bezeichnet!